MECHANISCHE FACTOREN.
De aanvangssnelheid kunnen we onderverdelen in:
-
Aanvangssnelheid aan het begin van de worp (Startsnelheid).
-
Aanvangssnelheid aan het einde van de worp (Afwerpsnelheid).
De Afwerpsnelheid is afhankelijk van:
-
Het niveau van de maximale / explosieve kracht.
-
Het technisch niveau van de werp(st)er.
Algemeen kan gesteld worden dat een hogere aanvangssnelheid ook een hogere afwerpsnelheid tot gevolg zou moeten hebben.
Echter het is van groot belang dat het technische niveau van de werp(st)er voldoende is om de snelheid ook goed om te kunnen zetten. Dit heeft alles te maken met een verbetering van de explosieve kracht. Het grootste probleem bij het bereiken van een hogere afwerpsnelheid is namelijk dat men onder versnelde omstandigheden toch dezelfde technische uitvoering moet kunnen blijven maken en dit is nu eenmaal niet eenvoudig door alleen het verbeteren van de techniek. Men moet dus ook gewoon sneller "spierarbeid" kunnen verrichten.
Dit probleem wordt mijns inziens zwaar onderschat door trainers.
Is het technische niveau beter geworden en is ook de explosieve kracht toegenomen, dan kan gesteld worden dat diezelfde werp(st)er ook met een hogere aanvangssnelheid zou moeten kunnen beginnen.
We spreken dan ook wel van een "optimale" aanvangssnelheid.
Uit onderstaande tabel blijkt hoe belangrijk de afwerpsnelheid van bijvoorbeeld het kogelstoten is. Hierbij is rekening gehouden met een konstante stijgingshoek van 42° graden en een konstante afwerphoogte van 2.30 meter.
| Afwerpsnelheid: | Behaalde Afstand: | |
| 11 m/sec. | 14.43m | |
| 12 m/sec. | 16.80m | |
| 13 m/sec. | 19.28m | Gegevens volgens |
| 14 m/sec. | 22.15m | L. Tutjowitsch. |
Uit bovenstaande tabel blijkt dat bij een relatief klein verschil van 1 m/sec. (13 en 14 m/sec.) er een wereld van verschil is in het behaalde eindresultaat. Immers het verschil tussen 19.38m en 22.15m is het verschil tussen een subtopper en een absolute wereldtopper.
De werp(st)er moet altijd streven naar een zo groot mogelijke lengte van de contactbaan, zodat er meer ruimte is om een zo hoog mogelijke versnelling van het werpmateriaal te krijgen. We spreken in dit geval ook wel van "optimale" lengte van de contactbaan.
Ook dit heeft alles te maken met het verbeteren van de techniek van het discuswerpen.
De beperkende factor is uiteraard het lichaam van de werp(st)er zelf. Iemand die een grote spanwijdte heeft die heeft bij een "optimale" techniek een langere contactbaan dan iemand met een kleinere spanwijdte.
Er moet gestreefd worden naar een verhoging van het explosieve krachtsniveau.
Dit heeft als voordeel dat de contactbaan sneller doorlopen kan worden, wat weer een hogere afwerpsnelheid tot gevolg heeft.
3. De Stijgingshoek.
In veel literatuur is te lezen dat een optimale stijgingshoek ofwel afwerphoek, ongeveer 36 tot 38 graden bedraagt.
Hierbij kan toch wel een kanttekening geplaatst worden.
Omdat de discus een platte schijf is heeft de windsterkte en windrichting hierop een zeer grote invloed.
Algemeen kan gezegd worden dat bij tegenwind recht van voren veel lager moet worden afgeworpen.
Bij wind van links moet ook lager worden afgeworpen.
Bij wind van rechts kan wel onder deze hoek worden afgeworpen.
Bij meewind kan zelfs hoger worden afgeworpen.
Uit onderstaande tabel blijkt dat de ideale afwerphoek bij het kogelslingeren 44 graden bedraagt. Hierbij speelt de windsnelheid of windrichting eigenlijk weinig of geen rol omdat de slingerkogel een ronde vorm heeft.
| Stijgingshoek: | Behaalde Afstand: | |
| 38 graden | 72.92m | |
| 40 graden | 73.78m | |
| 42 graden | 74.28m | |
| 44 graden | 74.46m | Gegevens volgens |
| 46 graden | 74.28m | L. Tutjowitsch. |
4. De Afwerphoogte.
De afwerphoogte is afhankelijk van:
-
Lengte van de werp(st)er.
-
Werponderdeel.
-
Technisch niveau van de werp(st)er.
Bij het discuswerpen is de afwerphoogte niet echt relevant, daar het voor een juiste technische uitvoering van de afworp niet van belang is dat er zo hoog mogelijk wordt afgeworpen.
Bij een ander werponderdeel zols het kogelstoten is dit wel degelijk van belang. Iedere centimeter dat de kogel hoger wordt afgestoten geeft een afstandswinst van ongeveer 1 cm.
Uit onderstaande tabel blijkt het verschil tussen afwerphoogte en de uiteindelijk geworpen afstand. Hierbij is rekening gehouden met een konstante afwerpsnelheid van 13 m/sec. en een konstante stijgingshoek van 41° graden.
| Afwerphoogte: | Gewopen Astand: | |
| 1.80m | 18.93m | |
| 2.00m | 19.11m | |
| 2.20m | 19.29m | |
| 2.40m | 19.48m | Gegevens volgens |
| 2.60m | 19.66m | L. Schmolinsky. |
Zodoende krijgt een grote werp(st)er al gauw enkele tientallen centimeters "gratis" ten opzichte van een kleiner iemand.
5. De Zwaartekracht.
De zwaartekracht heeft "theoretisch" een kleine invloed op de geworpen afstand.
Niet overal op aarde is de zwaartekracht namelijk even groot.
-
g = aan de evenaar ongeveer 9.78 m/sec.
-
g = in Amsterdam ongeveer 9.81 m/sec.
-
g = aan de polen ongeveer 9.83 m/sec.
Theoretisch zou dus aan de evenaar de geworpen afstand groter zijn dan aan de polen.
Het is echter in de praktijk onmogelijk om hier rekening mee te houden daar dit minimale verschillen met zich meebrengt.
Veel belangrijker is de wind die van invloed is op het werpmateriaal.
Stromingskrachten hebben bij het discuswerpen een ZEER GROTE invloed op de uiteindelijk geworpen afstand.
De wet van Bernouilly.
Deze wet vertelt ons dat verschillende snelheden van luchtdeeltjes, verschillende luchtdrukken veroorzaken. Daar waar de snelheid het hoogst is, is de druk het laagst en omgekeerd.
Aan de vorm van de discus is reglementair gesproken niet veel te verbeteren, daar deze discus aan voorgeschreven maten en gewichten moet voldoen.
Verder is de luchtweerstand op het materiaal afhankelijk van:
-
De afwerpsnelheid.
-
De windsnelheid.
-
De windrichting.
-
De vorm van het materiaal.
-
De omvang van het materiaal.
-
De aard van het materiaal (glad/ruw).
-
De massa van het materiaal.
-
De ligging van het materiaal.
Punten 1 t/m 7 zijn in een eerder stadium al behandeld.
Ten aanzien van punt 8, "De ligging van het materiaal", het volgende.
We kunnen een drietal verschillende hoeken onderscheiden die belangrijk zijn ten aanzien van de ligging van het materiaal ten opzichte van de horizontaal, t.w.:
-
De Stijgingshoek oftewel Afwerphoek.
-
De Neigingshoek.
-
De Invalshoek.
De stijgingshoek oftewel afwerphoek, is de hoek waarmee het werpmateriaal geworpen wordt ten opzichte van de horizontaal.
De neigingshoek is de hoek van de positie of ligging van het materiaal in de lucht ten opzichte van de horizontaal.
De invalshoek is het verschil tussen deze stijgingshoek en de neigingshoek.
Er zijn 3 verschillende situaties waaronder een discus geworpen kan worden:
-
invalshoek = 0
-
invalshoek = negatief
-
invalshoek = positief
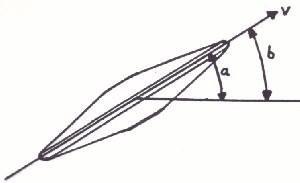 |
Een invalshoek die 0 is betekent dat de stijgingshoek (a) en neigingshoek (b) even groot zijn. |
||
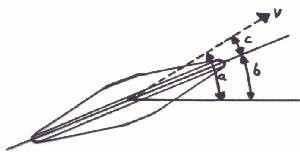 |
Is de stijgingshoek (a) groter dan de neigingshoek (b), dan spreken we van een negatieve invalshoek (c). |
||
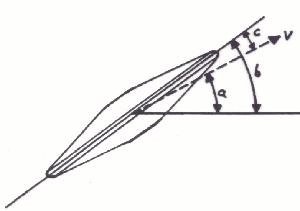 |
Is de stijgingshoek (a) kleiner dan de neigingshoek (b), dan spreken we van een positieve invalshoek (c). |
Bij het discuswerpen kan vanuit de positie van de werp(st)er gezien worden met welke invalshoek er is geworpen.
Kan men direct na de afworp het bovenste gedeelte van de discus zien dan is de invalshoek POSITIEF.
Kan men direct na de afworp het onderste gedeelte van de discus zien dan is de invalshoek NEGATIEF.
Kan men direct na de afworp eigenlijk niet het bovenste gedeelte en ook niet het onderste gedeelte van de discus zien dan is de invalshoek 0.
Onderstaande tabel geeft de invloed van de windrichting en de windkracht aan bij het kogelstoten.
Bij het discuswerpen is zo'n tabel niet te maken omdat de vorm van de discus dit niet toestaat. Een kogel is rond en heeft hierdoor altijd dezelfde stromingskrachten. Een discus heeft dat niet.
|
Windrichting: |
Windsnelheid: |
Kogeldoorsnede: |
Kogeldoorsnede: |
|
|
|
12 cm: |
13 cm: |
|
Wind tegen |
10 m/sec. |
21.50m |
21.38m |
|
Wind tegen |
5 m/sec. |
21.68m |
21.61m |
|
Wind stil |
0 m/sec. |
21.82m |
21.78m |
|
Wind mee |
5 m/sec. |
21.90m |
21.89m |
|
Wind mee |
10 m/sec. |
21.95m |
21.94m |
|
|
|
|
|
|
Gegevens volgens |
L. Tutjowitsch. |
|
|
© Piet Meijdam - Amsterdam
